Age: 6 Presentations: Putting Fractiosn in order from 1 to tenth, Matching Fractions From Whole to a Tenth Note: Here are my other posts on our
Tag: Math
Age: 7.75 Date: June 2, 2015 Presentation: Numerical Decanomial with Paper Rectangles and Squares After the Decanomial layout we did last week (or was it the
Age: 4.75 & 7.75 Presentations: Tables Layout Decanomial Layout: Finding Squares Adjusted Decanomial: Commutative Law Adjusted Decanomial: Tower of Jewels Stacking the cubes Even though
Age: 7.5 Presentation: Transformation of a Square, Passing from One Square to Another, Concept and Notation of Square Roots, Extracting a square root for numbers less
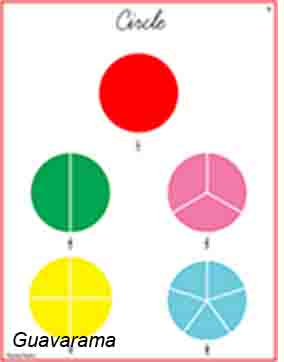
Update May 2020: You can. now get the charts here. After the confusion that was the fraction charts last semester, I sat down and re-did
My math class is chugging along. Once again 1/3 of the album is due and I’m madly catching up after taking 2 weeks off to
My first 1/3 of the math album was due tonight. I didn’t finish. But we all got an due date extension. But rather than working
Last month, I got really into wanting to find out how children learn/remember. The impetus was wondering if Anki would help Thumper learn her addition facts.
Update: I figured out how to make the fraction charts 6 months later. Here’s my post and pics of the final charts as well as
Ages: 4 & 7 Last week and this week, both Astroboy (4) and Thumper (7) got their introduction to fractions. In training, I was told that fractions